– Last update: 08 Dec 2023.

I’ll collect in the blog a few recent trends that help speed up inference of autoregressive models.

Jump to it:

> What happened to “Transformers are very optimal/parallelizable”

Ok, chill!

That is still the case, and will always be. But we mostly benefit from it in TRAINING. Inference though, is inherently sequential. I.e., say that \(p(. \mid .)\) represents the output distribution of the model, and given a prompt \(T\), you generate the first token autoregressively by sampling \(x_1 \sim p(.\mid T)\) and then to generate the second token you condition on both \([T, x_1]\), \(x_2 \sim p(.\mid T, x_1)\). There is simply (and sadly) no escape from this incremental design.

I guess no one is perfect after all, right?!

> Multi Query Attention (MQA):

This is a great paper, its idea could be summarized in one sentence, but the performance analyses that he provides are super interesting. I’ll only detail the analysis of the first section.

As a motivation, Gemini 1.0 was released on Dec 06 2023. Although they don’t disclose much about the architectural choices behind it, they made it clear that they’ve used MQA (pretty cool, huh?). As you see below, screen taken from the technical report.

MQA-gemini

Content:

TL;DR: Use only ONE key/value per multiple queries (i.e., drop the dim across the heads of K and V).

– Batched Multi-Head Attention (MHA, aka, Vanilla Attention):

Here’s the provided script for completeness: 

def MultiheadAttentionBatched(X, M, mask, P_q, P_k, P_v, P_o):
    """
    [...]
    P_q: a tensor with shape [h, d, k] # keep a look at the dim
    P_k: a tensor with shape [h, d, k] # keep a look at the dim
    P_v: a tensor with shape [h, d, v] # keep a look at the dim
    P_o: a tensor with shape [h, d, v]
    [...]
    """

    Q = tf.einsum("bnd,hdk->bhnk", X, P_q)
    K = tf.einsum("bmd,hdk->bhmk", M, P_k)
    V = tf.einsum("bmd,hdv->bhmv", M, P_v)
    [...]
    # the rest in un-changed in MQA.

– Performance analysis of Batched MHA:

– Incremental batched MHA (Inference):

Same as before, except here, we introduce and append the KV cache along the way.

def MHA(x, prev_K, prev_V, P_q, P_k, P_v, P_o):
    """Multi-Head Self-Attention (one step).
    
    Args:
    x: a tensor with shape [b, d]
    prev_K: a tensor with shape [b, h, m, k]
    prev_V: a tensor with shape [b, h, m, v]
    P_q: a tensor with shape [h, d, k]
    P_k: a tensor with shape [h, d, k]
    P_v: a tensor with shape [h, d, v]
    P_o: a tensor with shape [h, d, v]
    
    Returns:
    y: a tensor with shape [b, d]
    new_K: a tensor with shape [b, h, m+1, k]
    new_V: a tensor with shape [b, h, m+1, v]
    """
    q = tf.einsum("bd,hdk->bhk", x, P_q)
    new_K = tf.concat([prev_K, tf.expand_dims(
		tf.einsum("bd,hdk->bhk", M, P_k), axis=2)], axis=2)
    new_V = tf.concat([prev_V, tf.expand_dims(
		tf.einsum("bd,hdv->bhv", M, P_v), axis=2)], axis=2)
    logits = tf.einsum("bhk,bhmk->bhm", q, new_K)
    weights = tf.softmax(logits)
    o = tf.einsum("bhm,bhmv->bhv", weights, new_V)
    y = tf.einsum("bhv,hdv->bd", o, P_o)
    
    return y, new_K, new_V

– Analysis of Incremental batched MHA (Inference):

Similarily to the analysis in the batched MHA, we get for \(n\) generated tokens:

Now, it’s tricky to push the ratio to be \(\ll 1\). We can’t just increase the batch size \(b\) as we are contsrained by the memory size. But also, when \(n \approx d\), memory bandwidth would be a bottleneck for performance. So, what do we do now? The author proposes, Multi-Query Attention (MQA). MQA radically removes the heads (h) dimension off \(K\) and \(V\).

– Multi Query Attention (MQA):

As you can see in the script below, MQA is literally MHA without the h dimension in K, and V.

def MultiQueryAttBatched(X, M, mask, P_q, P_k, P_v, P_o):
    """
    Args:
    [...]
    P_k: a tensor with shape [d, k]
    P_v: a tensor with shape [d, v]
    [...]
    """
    Q = tf.einsum("bnd,hdk->bhnk", X, P_q) #h is still there in the output dim
    K = tf.einsum("bmd,dk->bmk", M, P_k)   #h is dropped 
    V = tf.einsum("bmd,dv->bmv", M, P_v) #h is dropped 

    logits = tf.einsum("bhnk,bmk->bhnm", Q, K)
    # we recoved the same dim of the logits as the MHA,
    # everything is the same as MHA from now onwards.
    [...]

– Incremental MQA (Inference) Differences in code are marked as #no h.

def MultiquerySelfAttentionIncremental(x, prev_K, prev_V, P_q, P_k, P_v, P_o):
    """
    Args:
    x: a tensor with shape [b, d]
    prev_K: a tensor with shape [b, m, k]  #no h
    prev_V: a tensor with shape [b, m, v] #no h
    P_q: a tensor with shape [h, d, k]
    P_k: a tensor with shape [d, k] #no h
    P_v: a tensor with shape [d, v] #no h
    P_o: a tensor with shape [h, d, v]
    [...]
    new_K: a tensor with shape [b, m+1, k] #no h
    new_V: a tensor with shape [b, m+1, v] #no h
    """
    q = tf.einsum("bd,hdk->bhk", x, P_q)
    K = tf.concat([prev_K, tf.expand_dims(tf.einsum("bd,dk->bk", M, P_k), axis=2)], axis=2)
    V = tf.concat([prev_V, tf.expand_dims(tf.einsum("bd,dv->bv", M, P_v), axis=2)], axis=2)

    logits = tf.einsum("bhk,bmk->bhm", q, K) 
    # we revoved the dim `bhm`, the rest is same as before MHA.
    [...]

– Performance analysis for incremental MQA (Inference)

For \(n\) generations:

Here we see that the problematic fraction \(\frac{n}{d}\) that we encountered in incremenral-MHA, is further devided by h… which helps tremendessly with performance.

I spent too much on this paper, here are some final notes:

> Grouped Query Attention:

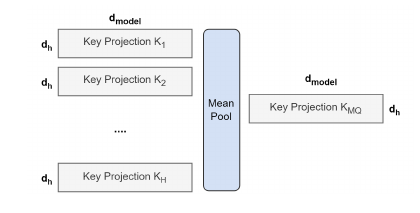
– Uptrainig from MHA to MQA happens in 2 steps:

  1. Convert checkpoint (snapshot of weights)
  2. Additional pre-training on a small percentage \(\alpha\) to adapt to the new structure.
    • They uptrained with \(\alpha = 0.05\) of the original pre-training steps of T5.

projection

Final interesting takes:

Coincid.. Gemini just dropped, and one of the few details about the architeture is that they used MQA… , pretty cool, huh??

– Grouped Query Attention:

Instead of all queries of an attention layer having the same key/value (MQA), we group queries into sub-groups that share the key/value (Check screen 1 below).

Comparison figure: comparison

– Final notes:

GQA  » Increase in inference speed && Reduces memory requirement during decoding.  » Higher batch size » Higher throughput

> Sliding Window Attention:

TODO

Relevent literature: Longformer, Sparse Transformers.

Vanilla attention scales quadratically with long sequences (Quick Why: with each input of the sequence (length n), you compute n weight/ reformulate this.)

– Longformer attention combines:

  1. Windowed attention (local) \(\rightarrow\) build a contextualized representation.
  2. End task global attention \(\rightarrow\) build full sequence representations for prediction.

Attention pattern:

  1. Sliding windon of fixed size around each token \(\implies\) attention matrix is sparsified.
    • Q: Is it literally masked? Q = Q’ x Mask ? Yes/No.
  2. x

– Sparse Transformers:

TL;DR: Add more sparsity to you attention weights. By shortening your attention span. Instead of accessing all you past, access only up to a window \(W\) (not really, they defind a pattern of “attendence”, will get to it later, the change the usual mask).

Section 4.2 is so well written, that I’m technically going to be re-writing it.

Vanilla attention (this is a mathpix test, looking fine on markdown so far):

\[\begin{gathered} \operatorname{Attend}(X, S)=\left(a\left(\mathbf{x}_i, S_i\right)\right)_{i \in\{1, \ldots, n\}} \\ a\left(\mathbf{x}_i, S_i\right)=\operatorname{softmax}\left(\frac{\left(W_q \mathbf{x}_i\right) K_{S_i}^T}{\sqrt{d}}\right) V_{S_i} \\ K_{S_i}=\left(W_k \mathbf{x}_j\right)_{j \in S_i} \quad V_{S_i}=\left(W_v \mathbf{x}_j\right)_{j \in S_i} \end{gathered}\]

> Flash Attention:

TODO

This 34 pages idea, wins the price of “Minimum innovation, maximum results– Ilya Sutskever”

One of the ideas: Basically, instead of moving KV’s around, just recompute them at backprop.

Why: Compute capabilities on GPUs is 2 orders of magnitude higher than memory. recompute is easy, moving data and storing it in GPUs is hard. Q: I thought OpenAI was already doing this, in their 2019 paper. Investigate this!!

> Notes on Mistral 7B:

The ratio of \(\frac{\text{ideas}}{\text{pages}}\) in the Mistral 7B is too high. It combines efficiently all the techniques that are mentioned above. Additionally, they use:

Set the cache size to a value \(W\), and store the keys and values at step \(i\) at position \(i \equiv W\) (modulo) \(\implies\) starting from step \(W\), cache get overwritten with new values.

Why is it fine to do so: because we add positional encoding before, so it doesn’t really matter where do you store, attention is a “set” operation.

I don’t get this yet. Check it later!

(Of course it’s related to KV cache.)

(pre-fill, is computing the KV of the prompt, which is already available in advance, hence we can chunk it, etc.)

(Chunking: Split the prompt size in chunks of size \(W\) (window size of the attention)  » Then what?)

> Speculative decoding:

– Quick Terminology:

– Main obsevation:

– Main idea:

Autoregressive sampling is memory bandwidth bound:

Why is scroring a draft continuation has \(\sim\) latency to generating a token.

TODO

Imagine having a draft model (typically fast/small), and a target model, typically big (think of the former as a Llama 7B, and the latter as a Llama 70B).

Speculative decoding in a nutshell:

  1. Generate a sequence of \(K\) (~ 4/5) tokens using the draft model.
  2. Scoring the the sequence using the target model.
  3. Accept/Reject the proposed sequence using a rejection sampling inspired technique, that hopefully recovers the target model output distribution.

Useful links:

TODO: